在这个撸猫成风的年代，薛定谔的猫也跟着成为了大概是猫史最有名的猫之一了。

虽然现在提起它，刷刷猫猫表情包的时候人们大概只是想要戏谑和玩笑，但是在科学史上，那个盒子里藏着光怪陆离的量子理论和量子的世界，人们对于薛定谔猫这个悖论的手足无措，恰好反映了当时人们对于微观和宏观，确定性和不确定性以怎样的方式相互作用并纠缠在一起而困惑。

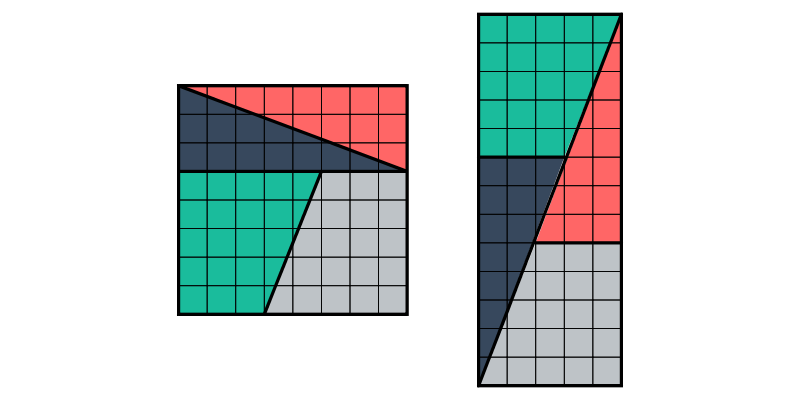
左边 8x8 的正方形，看上去和右边 5x13 的长方形面积一样大，难道 64=65？在科学发展的漫漫长河之中，人们对于概念的困惑并不只有这一个，因此提出的悖论也层出不穷，比如飞矢不动，麦克斯韦妖，薛定谔的猫，双生子佯谬等。今天的我们来看看，关于悖论，除了薛定谔的猫以外，还有哪些神奇的东西。

克莱因悖论

Klein Paradox

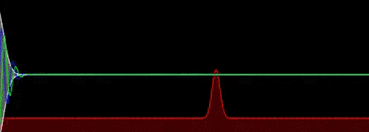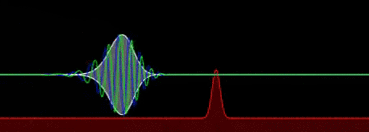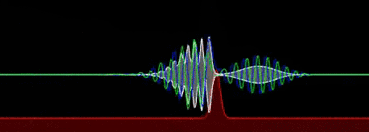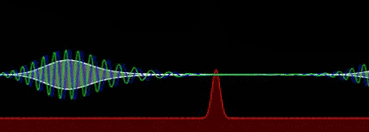
计算模拟的波包在经过势垒时发生透射和反射熟悉量子理论的话都知道量子隧穿的概念。正如我们常常用来比喻的“崂山道士”那样，微观的粒子具有穿墙术，有机会能够跨越能量的崇山峻岭，来到山的那一头。当我们把一个粒子甩向墙壁的时候，薛定谔方程一般会求解出粒子有一定几率在界面会发生反射——形象点理解的话，这个崂山道士学艺不是很精，。正如我们常常用来比喻的“崂山道士”那样，微观的粒子具有#FormatStrongID_9#，有机会能够跨越能量的崇山峻岭，来到山的那一头。当我们把一个粒子甩向墙壁的时候，薛定谔方程一般会求解出粒子有一定几率在界面会发生反射——形象点理解的话，这个崂山道士学艺不是很精，。

穿墙术，来自《崂山道士》在1928年的时候，狄拉克提出了狄拉克方程，把狭义相对论引进到了量子力学当中，并预言了正电子的存在。克莱因用狄拉克方程求解了上面提到的量子隧穿的问题，结果惊人地发现，对于无质量的，遵守狄拉克方程的粒子而言，在一定条件下，势垒对于它们而言是透明的。这意味着，这些粒子的穿墙术有着 100% 的成功率。

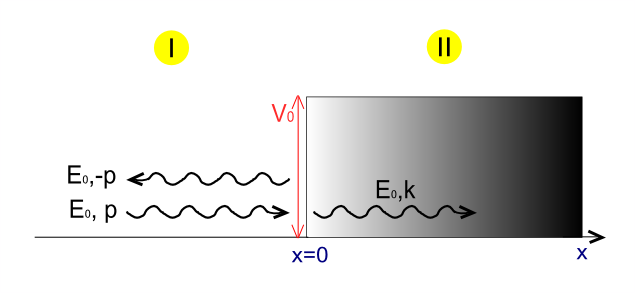
用狄拉克方程计算微观粒子能否穿墙当然，如果对于有质量的，遵守狄拉克方程的粒子而言，面对势垒，粒子大部分时候都还是保持了部分穿透的特性。可以想象，当势垒比起粒子本身的质量（质量与能量通过质能方程进行换算）大得多的时候，我们就回到了无质量的情形，粒子面对越来越高的势垒，反而越来越接近100%透射。你墙壁加得越高，跑出来的几率也变得越大。

给一张帅气的卢瑟福肖像画克莱因悖论并不只是一个理论模型的计算，实际上它还打过卢瑟福的脸。在卢瑟福做完了金箔的 α 粒子的散射实验，发现原子内部大部分都是空的以后，还对 α 粒子进行了长期的研究，最后发现了原子核中，一部分是由质子构成的。他在1920年发表题为“原子的构造”（The building up of atoms）的演说，提出原子核是由带正电的质子和带负电的电子所组成的。

但是你越想在原子核那么小的地方里关住电子，这些电子就跑得越厉害。假如原子核内只有质子和电子，根据克莱因悖论，电子大概早就跑干净了，卢瑟福的原子核模型不攻自破。直到1932年，查德威克发现了中子，人们才最终明白原子核是由质子和中子构成的。

亚里士多德圆轮悖论

Aristotle's Wheel Paradox

▲拉斐尔所绘雅典学院

图中正中间蓝衣即为亚里士多德在古希腊的时候，亚里士多德考虑了一件很好玩的事情。我们搞两个直径不相同的圆轮，把它们的圆心重叠在一起，在地面上做无滑动的纯滚动时，可以看到，两个圆的底部各自都划过了一条直线。两个圆的周长显然并不相同，但是两个圆的底部却划过了相同的距离，这确实是一件令人头大的事情。

按照一一对应的关系，似乎圆的周长应该都相等当然，你如果觉得上述的滚动说法实在不是那么好理解的话，你也可以想象从两个圆的共同圆心处引出一条射线，依次与内圆和外圆相交。这意味着对于内圆上的任何一个点，我们都能找到外圆上的唯一的一个点与之对应。从“朴素”的数学观点来看，就像聚沙成塔一样，如果两个沙堆里的沙子都是一一对应的话，那显然这两堆沙子应该一样大才对。然而内圆和外圆周长，真的不一样啊。

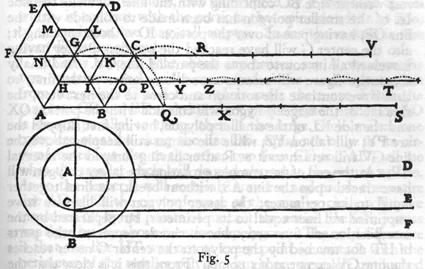
▲图片取自伽利略的对话录

无独有偶，伽利略也思考过这个问题。伽利略走的是无穷逼近的路子。如果我们考虑的不是两个同心的圆，而是两个同心的正六边形的时候。在正六边形不断翻转的过程中，我们可以想象，下面的轨迹会被大的正六边形的边完全覆盖，但是上面的那条轨迹，会被跳着被小的正六边形的边接触。如果我们考虑极限，那么亚里士多德圆轮悖论里面看似一样的两条轨迹，实际上下两条轨迹并不相同。假设我们有一个「足够大」的放大镜，。伽利略走的是#FormatStrongID_26#的路子。如果我们考虑的不是两个同心的圆，而是两个同心的正六边形的时候。在正六边形不断翻转的过程中，我们可以想象，下面的轨迹会被大的正六边形的边完全覆盖，但是上面的那条轨迹，会被跳着被小的正六边形的边接触。如果我们考虑极限，那么亚里士多德圆轮悖论里面看似一样的两条轨迹，实际上下两条轨迹并不相同。假设我们有一个「足够大」的放大镜，。

通俗地说，测度把每个集合映射到非负实数来规定这个集合的大小：空集的测度是0；集合变大时测度至少不会减小（因为要加上变大的部分的测度，而它是非负的）。

上述的这些关于无穷的思考启发了康托尔发明了集合论，就像在论证偶数的个数等于整数的个数那样：将所有的偶数除以2，就等到了所有整数；把所有的整数乘以2，就得到了所有的偶数；每个整数都唯一对应了一个偶数。

亚里士多德的圆轮上的点的数量也确实是相等的。但是点的数量和周长之间并没有什么绝对的关系，而这样也正是让我们思考最为困惑的地方。因此，数学家们还发展了测度论，用来对长度、面积、体积进行严格数学定义。

编辑：沈湫莎

责编：顾军

来源：中科院物理所微信公众号